项目研究和实验的目的、内容和要解决的主要问题
1. 项目研究目的:
如何利用先进的交通管理系统ATMS、先进的交通信息服务系统ATIS,改进快速路交通运行条件,提升通行效率,是当前许多特大、大型城市面临的重要课题。优秀的ATMS和ATIS系统必须依赖于准确、实时的交通状态检测、估计和预测,因此,针对我国城市快速路典型的道路、交通流特征,充分利用现有的交通流检测手段,运用合理的数据挖掘处理技术,准确快速估计、预测快速路的交通流状态,对于改进快速路交通运营管理十分重要。
本课题结合蓝牙数据,GPS浮动车数据,以及断面固定式检测数据(微波检测仪),综合交通流理论的基本原理和快速路交通运行的实际特点, 采用数据融合技术,深入研究城市快速路的交通态势检测和评估的多个关键理论与方法,最终实现对交通流状态的估计、对交通发展趋势的预测、以及对交通事故的检测。
与单源数据相比,多传感器数据进行融合可得到统计上的优势,使用多传感器数据还可以提高精度。
(l)采用数据融合技术可以获得更全面的交通流的特征信息
数据融合后,可以获得任何单一交通流信息采集方法不能获得的其它的交通流特征信息,增加了交通流特征信息、的维度。
(2)采用数据融合技术可以获得更加精确的交通流信息
采用单一交通信息采集方法得来的数据质量容易受到采集设备,天气等客观
因素的影响,而采用多种交通流信息采集方法可以在一定程度上克服客观因素的
影响。
(3)采用数据融合技术可以获得更加准确的交通运行状态评价结果
融合技术使各单一的交通流信息采集方法相互之间取长补短,因此融合后的数据比单一方法流采集的数据更准确。
基于此,本课题的研究构思如下:
(1)对现有相关研究成果的总结分析基础上,分析其不足,总结经验。
(2)采集数据,对数据源进行客观分析,包括各源数据采集方法及具体数据信息的介绍。
(3)对采集到的数据进行融合,研究最实用的融合算法,
(4)对经过融合处理的评价结果和未经融合处理的评价结果以及由前端融
合和后端融合处理得到的两个结果进行比较分析,给出结论和建议。
(5)采用计算机编程对程序的设计进行实现。
(5)通过得到的融合数据对交通事故进行检测。
2.研究内容:
利用卡尔曼滤波进行多源数据融合,进而估计城市快速路的交通状态,同时对比基于多源数据融合和基于单一数据估计的结果精度。
2.1 基于LWR模型的快速路交通流的刻画
将路段划分为I个元胞(每个长度为 ,记作i),时间划分成H个时间步(每个时长为 ,记作i),时间划分成H个时间步(每个时长为 ,记作h)。为了满足Courant-Friedrichs-Lewy(CFL)稳定性条件,没有车辆可以在一个时间步中行驶出一个元胞,即 ,记作h)。为了满足Courant-Friedrichs-Lewy(CFL)稳定性条件,没有车辆可以在一个时间步中行驶出一个元胞,即 。 。
 (1) (1)
初始条件:
 (2) (2)
边界条件:
 (3) (3)
—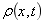 :t时刻,x处密度。 :t时刻,x处密度。
2.2 基于卡尔曼滤波算法的交通流状态估计
卡尔曼滤波利用递归方法解决随机线性离散系统的状态或参数估计问题。由状态方程和观测方程组成,并利用状态方程的递推性,按线性无偏最小均方误差估计准则,对状态变量作最佳估计。
(1)状态方程
如果只考虑整个路段处于自由流动或拥挤状态,状态方程如下:
 (4) (4)
— 是时间步h的元胞i的密度。 是时间步h的元胞i的密度。
其中δ= w / ,w是后向冲击波速度。 方程(4)假设每个元胞长度相等和同样的基本图,在路段中没有车辆的驶入驶出(即没有匝道)。 ,w是后向冲击波速度。 方程(4)假设每个元胞长度相等和同样的基本图,在路段中没有车辆的驶入驶出(即没有匝道)。
状态方程矩阵形式如下:

(5)
向量 是在时间步h的状态向量,矩阵Ah和Bh是时变的,它们在时间步h处取决于模式m。在自由流模式中m = 1,在拥塞模式中m = 2。wh表示状态方程的误差(由于错误或遗漏的计数引起,例如车辆变道)。输入uh是标量,并且与在计算域的边界处获得的测量相关(用于分别计算自由流或拥塞模式下的第一或最后一个元胞的密度)。事实上,如果整个路段在自由流或拥挤模式下: 是在时间步h的状态向量,矩阵Ah和Bh是时变的,它们在时间步h处取决于模式m。在自由流模式中m = 1,在拥塞模式中m = 2。wh表示状态方程的误差(由于错误或遗漏的计数引起,例如车辆变道)。输入uh是标量,并且与在计算域的边界处获得的测量相关(用于分别计算自由流或拥塞模式下的第一或最后一个元胞的密度)。事实上,如果整个路段在自由流或拥挤模式下:

(6)

(7)
其中 、 、 为边界条件; 为边界条件; 是初始条件。 是初始条件。
(2)观测方程
观测方程如下:

(8)
yh是观测矢量,vh是测量误差。卡尔曼滤波还假设wh和vh是独立的,且服从均值为的正态分布。Ch的大小取决于h时间步处的拉格朗日观测值来自哪里,并且它仅包含0和1(假定可以从拉格朗日传感器观测到局部密度)。拉格朗日观测来自不同的元胞,并且在连续时间步长之间的观测数量可能不同。因此,等式(8)中的观测矢量y h将在不同的时间步长具有不同的维度。后者意味着矩阵Ch也将在每个时间步长具有不同的维度。
(3)递归方程
卡尔曼滤波递归方程如下:
 (9) (9)
 (10) (10)
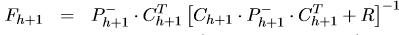 (11) (11)
 (12) (12)
 (13) (13)
 :kh的先验状态估计; :kh的先验状态估计;
 :kh的后验状态估计; :kh的后验状态估计;
 :先验估计误差协方差矩阵; :先验估计误差协方差矩阵;
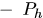 :后验估计误差协方差矩阵。 :后验估计误差协方差矩阵。
假定已知初始条件 和 和 。 Q和R分别是过程协方差矩阵和测量误差协方差矩阵。 Fh是时间步h的卡尔曼增益。矩阵Ch在每个时间步长具有不同的维度,这意味着协方差矩阵R的维数可变。 。 Q和R分别是过程协方差矩阵和测量误差协方差矩阵。 Fh是时间步h的卡尔曼增益。矩阵Ch在每个时间步长具有不同的维度,这意味着协方差矩阵R的维数可变。
在每个时间步开始时,交通状态需要被识别(为了决定矩阵A和B)。一旦在时间步h + 1的开始已经识别出模式,则使用公式(9)和(10)来分别获得先验密度估计和协方差(使用从检测器站提供的欧拉数据)。此时拉格朗日数据将提供给模型,即一些元胞在时间步h + 1处的观测密度是已知的(在时间步h + 1的拉格朗日传感器的数量和位置将决定观测密度的数量和哪些元胞的密度被观测)。利用该信息,可以构造观测矢量  和矩阵 和矩阵 。然后,使用公式(11)计算卡尔曼滤波器增益。最后,利用式(12)和(13)分别得到后验密度估计和后验估计协方差矩阵。若在h+1没有观测数据,矩阵 。然后,使用公式(11)计算卡尔曼滤波器增益。最后,利用式(12)和(13)分别得到后验密度估计和后验估计协方差矩阵。若在h+1没有观测数据,矩阵 等于0,意味着卡尔曼增益也是0,因此后验密度估计等于先验密度估计。 等于0,意味着卡尔曼增益也是0,因此后验密度估计等于先验密度估计。
3. 拟解决的主要问题:
(1)交通流状态数据的采集
(2)数据处理及融合方法
(3)基于卡尔曼滤波的快速路交通状态估计
(4)基于交通流数据的交通事故发生预测
(5)设计程序的实现
|